Pattern matching with std::variant, std::monostate and std::visit (C++17)

This article presents two practical examples of the basic pattern-matching capability of C++17 with std::variant, std::visit and std::monostate. The first example demonstrates the idea on a quadratic equation. The second one presents a line-line intersection, a similar example with classes.

Roots of a quadratic equation

This example presents the solution of a quadratic equation, which has either 2, 1 or 0 roots in the real number domain. A non-existent solution is represented by std::monostate() which is used for cases when std::variant does not contain a value.

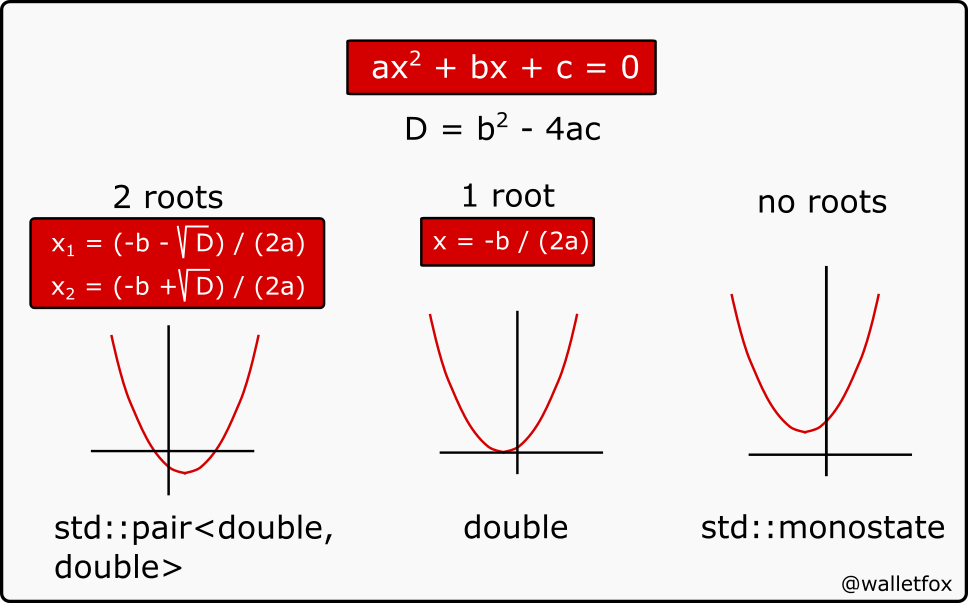
We are going to use a type alias var_roots for our variant to make the code more readable. To simplify type matching with std::visit, we introduce a hint overloaded that guides the deduction of template arguments supplied to the constructor.

Note: More on the hint overloaded can be found in the paper P0051R2 for LEWG and in this post by Marius Elvert.

#include <iostream>
#include <variant>
#include <cmath>
 
template<class... Ts> struct overloaded : Ts... { using Ts::operator()...; };
template<class... Ts> overloaded(Ts...) -> overloaded<Ts...>;

using var_roots = std::variant<std::pair<double,double>, double, std::monostate>; 

var_roots computeRoots(double a, double b, double c){
    auto d = b*b-4*a*c; // discriminant
    if (d > 0.0){
        auto p = sqrt(d) / (2*a);
        return std::make_pair(-b + p, -b - p);
    }
    else if (d == 0.0)
        return (-1*b)/(2*a);
    else
        return std::monostate();
}

void printQuadResult(const var_roots& v){
    std::visit(overloaded {
            [](const std::pair<double,double>& arg) { 
                        std::cout << "2 roots found: " 
                                  << arg.first << " " << arg.second << '\n'; },
            [](double arg) { std::cout << "1 root found: " << arg << '\n'; }, 
            [](std::monostate) { std::cout << "No real roots found.\n"; },
    }, v);
}

int main() {
    printQuadResult(computeRoots(1,0,-1));  // 2 roots found: 1 -1
    printQuadResult(computeRoots(1,-2,-2)); // 2 roots found: 3.73205 0.267949
    printQuadResult(computeRoots(1,6,9));  // 1 root found: -3
    printQuadResult(computeRoots(1,-3,4)); // No real roots found.
}

Could this be of interest to you?

Intersection of two lines

This is a similar example with structs. For simplification, lines are represented by their slope and Y-intercept. The line-line intersection problem has three possible solutions, lines either have one, none or an infinite number of intersection points (in case they are identical). Parallel lines with no intersection points are represented with std::monostate(). Identical lines are represented by INFINITY, which is a double. This is technically not completely correct (we use a double to represent an infinite set of points) but it serves the purpose.

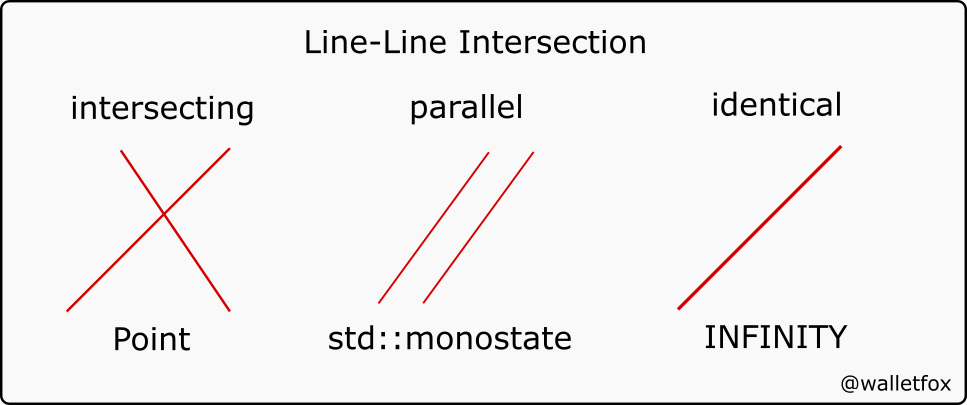
#include <iostream>
#include <variant>
#include <cmath>
 
template<class... Ts> struct overloaded : Ts... { using Ts::operator()...; };
template<class... Ts> overloaded(Ts...) -> overloaded<Ts...>;

class Point {
public:
    Point(): m_x(0.0), m_y(0.0){} 
    Point(double x, double y) : m_x(x), m_y(y){}
    double x() const {return m_x;}
    double y() const {return m_y;}
private:
    double m_x;
    double m_y;
};

class Line {
public:
    Line(): m_s(1.0), m_y(0.0){}
    Line(double s, double y): m_s(s), m_y(y){}
    double slope() const {return m_s;}
    double yintercept() const {return m_y;}
private:
    double m_s; // slope
    double m_y; // y-intercept
};

// 1 point, infinity, no points
using var_points = std::variant<Point, double, std::monostate>

var_points computeIntersect(const Line& l1, const Line& l2){
    auto slopeDiff = l1.slope() - l2.slope();
    if(slopeDiff == 0.0){
        if(l1.yintercept() == l2.yintercept())
            return INFINITY; // identical
        return std::monostate(); // parallel
    }
    else {
        auto intersectX = (l2.yintercept() - l1.yintercept()) / slopeDiff;
        auto intersectY = l1.slope() * intersectX + l1.yintercept();
        return Point(intersectX, intersectY); // 1 intersection
    }
}

void printIntersect(const var_points& v){
    std::visit(overloaded {
            [](double inf) { std::cout << "Lines are identical.\n"; },
            [](std::monostate) { std::cout << "Lines are parallel. \n"; },
            [](const Point& p) { std::cout << "Intersection found: " 
                                           << p.x() << " " << p.y() << '\n'; },   
    }, v);
}

int main() {
    printIntersect(computeIntersect(Line(2.0,3.0), 
                                    Line(-0.5,7.0))); // Intersection found: 1.6 6.2
    printIntersect(computeIntersect(Line(2.5,3.0), 
                                    Line(2.5,8.0))); // Lines are parallel.
    printIntersect(computeIntersect(Line(-1/2.0,3.0), 
                                    Line(-0.5,3.0))); // Lines are identical.
}

Tagged: C++